The Trick
After discussing multiplication of numbers by 11, let us discuss another math shortcut method which is very popular among kids and teenagers. This is squaring numbers ending in 5.
For kids, you can read the first portion of this post if you want to learn the trick, and read further if you want to learn the mathematics behind the trick.
Remember: it is cool if you know the trick, but it is even cooler if you know why it works. Mathematics is not just knowing the method, but also knowing the reasons.
Math Shortcut on Squaring Numbers Ending in 5
The algorithm is squaring numbers ending in 5 is the following.
1.) Multiply the ones digits. That is 5 x 5 since they both of them in 5. Write 25 as product as shown below. The last two digits of this trick is always 25.
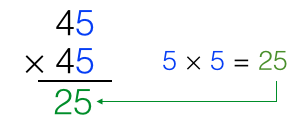
2.) Add 1 to one of the tens digit.
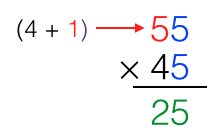
3.) Multiply the sum into by the tens digit of the other number. Here, we multiply 3 in (2) by 2.
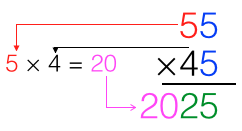
That means that the 45× 45 = 2025.
Example 2: What is 35 × 35?
First, our last two digits is 5 × 5 = 25. Then, instead of 3× 3, we increase one of the factors by 1. That is 4 × 3 = 12. So, the correct answer 35 × 35 = 1225.
Now, why does this trick work? Will it work in all possible cases? Try other 2-digit ending in 5 and check the product manually or use a calculator.
The Secret
The secret of this trick needs a little Algebra. If you have taken Algebra 1, then this explanation is fine for you.
Two digit numbers can be expressed as 10t + u, where t and u are the tens and units respectively. Here are a few examples.
28 = 20 + 8 = 10(2) + 8
74 = 70 + 4 = 10(7) + 4
96 = 90 + 6 = 10(9) + 6
This means that if we have a number which has tens digit as n, then squaring a number ending in 5 will look like
(10n + 5)(10n + 5).
Multiplying, we have
100n2 + 100n + 25.
Since our last two digits in the multiplication above is 25, if we get 25, we are only left 100n2 + 100n which is hundreds digit.
We can factor 100n2 + 100n as 100 n(n + 1).
Notice: n is equivalent to 4 in our first example and the n + 1 is the equivalent to 5. This means that we always have to add 1 to n in one of the tens digit and then multiply to get the product.
